dancing links 的简单介绍及应用
很早以前写的一个文章的初稿。可惜的是底稿找不到了。。。
很多内容都没有修正和添加,不过大体内容差不多,有兴趣的将就着看看吧。
地址如下:
http://acm.whu.edu.cn/blog/read.php?90
圆的面积并
By momodi at 2009.11
摘要
设想生活中往往需要知道很多图形的面积,但是当图形有多个的情况下,我们怎么知道这些图形的面积的并集呢? 现实中的图形往往可以转化成一些多边形和圆的组合. 本文介绍了一个O(n^2logn)求圆的面积并的算法. 并将其拓展,使其可以求得复杂现实图形的并集.与经典的扫描线相比,本文介绍的方法效率高,占用空间少,容易实现及拓展,而且几乎没有难以处理的几何特殊情况.
有向面积和简单多边形的面积
凸多边形的面积可以通过三角剖分(如下图所示)得到的每一个三角形的面积相加来得到.
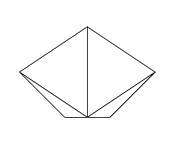
上图中是以多边形内部的一个点为中心来进行的三角剖分,剖分出来的所有三角形后,只要把面积简单相加就可以了. 利用有向面积,我们可以把这个点取在多边形外部.
我们可以用如下公式来表示凸多边形的面积:
![]() )
)
½(XkYk+1 – Xk+1Yk)便是一个以原点为中心点进行剖分出来的三角形的有向面积. 其实,这便是两个向量的叉积的值一半.
如果求得的总面积为正, 那么多边形的点集为逆时针存储. 否则为顺时针.
这个公式同样适用于简单多边形. 并不要求多边形一定是凸的.
圆的面积并的算法
先来观察一个图形:

此图表示了三个圆形的并. 我们在圆上随机选取了一些点, 并且使其包含圆与圆之间的交点. 我们选取了最外层的点对, 并将其用线段连接起来.
从图中我们可以看出, 我们将这个图形剖分成了一个简单多边形和一些半月. 对于这个图形, 我们只要求出简单多边形的面积再加上所有的半月的面积. 便是这三个圆形的面积并.
我们将这个做法一般话.
1. 去掉重复的圆形并求出圆与圆之间的所有交点的点集Ω.
2. 对于任意一个圆, 点集Ω中对应于这个圆的交点将其离散化成一个个小圆弧. 如果圆弧的角度大于90度, 则添加虚点, 将其分解成两个小圆弧.
3. 规定逆时针为圆弧的正方向.对于所有的小圆弧, 判断其是不是被其他圆所覆盖过. 取出所有的未被覆盖过的圆弧.
4. 对于圆弧的两个端点连接而成的线段, 将其看成简单多边形的一条边, 把其构成的有向面积加到总面积里面.
5. 对于圆弧所构成的半月, 将其面积直接加到总面积里面.
判断小圆弧是不是被其他的圆覆盖的方法, 可以取出这个圆弧的特征点(比如圆弧的中点), 然后判断这个点是不是被其他圆所覆盖.因为小圆弧是用所有交点离散化之后的,所以小圆弧上除了端点之外都有共同特征,因而上述方法是正确的.
这个做法是否适用于所有的情况呢? 且看如下图形:

对于这种内空的情况, 我们的做法也是适用的.因为对于内部的图形来说. 我们求得的多边形是顺时针的. 所以最后的总面积相当于减掉了这部分面积. 下面让我们来证明这个做法的正确性.
算法复杂度
对于每一个圆来说, 其圆上的点最多是O(n)个. 也就是说圆上那个最多有O(n)条小圆弧.每一个圆弧判断是否被覆盖的复杂度是O(n). 也就是说总的复杂度是O(n^3), n为圆的个数.
实际上,这样裸露的实现方法浪费了大量的有用信息,所以算法复杂度过高.我们可以通过改进圆弧是否被覆盖的方法来优化时间复杂度.
算法的优化
对于一个圆形来说,把他和所有其他圆形的交点求出来之后我们可以知道这个圆形上所有被覆盖掉的极角区间.我们可以用O(nlogn)的算法来求出极角区间的并.再用总的区间减掉这个并集,剩下的就是我们所要知道的所有未被覆盖过的小圆弧.
经过这样的优化,时间复杂度变为了O(n^2logn).而且这个logn的出现是因为区间并需要排序.如果用非基于比较的排序算法的话,时间复杂度可以降低为O(n^2).
算法的拓展
相信读者已经能够看得出, 此算法有一定的通用性. 如果把圆换成多边形, 最终算法的框架也是一样的. 只是细节上会有所变化.甚至可以是求圆和多边形等混合图形的并集.