http://poj.grids.cn/contest/1774/problem-A/

这个题目是我出的，题意写的有点晦涩-.-!

不过简单表述起来还是挺简单的。

就是在一个圆上进行切割，每一次切割都要跨过整个圆。然后需要检查切割线，检查切割线的方法就是碰触切割出来的每一个小块。

说白了就是小块为点，相邻的小块连边，然后问进行点涂色，使得每一个边的两个端点至少有一个是涂色过了的。

解法：

通过一系列比较麻烦的几何处理之后，所求出来的图是一个二分图。然后求得二分匹配就是答案。

关于这个图是二分图的证明也有比较形象的理解，就是这个图是明显没有奇环的，所以就是二分图咯。。。

By momodi at 2009.11

摘要

设想生活中往往需要知道很多图形的面积,但是当图形有多个的情况下,我们怎么知道这些图形的面积的并集呢? 现实中的图形往往可以转化成一些多边形和圆的组合. 本文介绍了一个O(n^2logn)求圆的面积并的算法. 并将其拓展,使其可以求得复杂现实图形的并集.与经典的扫描线相比,本文介绍的方法效率高,占用空间少,容易实现及拓展,而且几乎没有难以处理的几何特殊情况.

有向面积和简单多边形的面积

凸多边形的面积可以通过三角剖分(如下图所示)得到的每一个三角形的面积相加来得到.

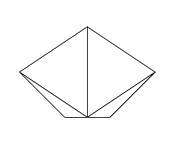
上图中是以多边形内部的一个点为中心来进行的三角剖分,剖分出来的所有三角形后,只要把面积简单相加就可以了. 利用有向面积,我们可以把这个点取在多边形外部.

 我们可以用如下公式来表示凸多边形的面积:

)

½(X_kY_k+1 – X_k+1Y_k)便是一个以原点为中心点进行剖分出来的三角形的有向面积. 其实,这便是两个向量的叉积的值一半.

如果求得的总面积为正, 那么多边形的点集为逆时针存储. 否则为顺时针.

这个公式同样适用于简单多边形. 并不要求多边形一定是凸的.

圆的面积并的算法

先来观察一个图形:

此图表示了三个圆形的并. 我们在圆上随机选取了一些点, 并且使其包含圆与圆之间的交点. 我们选取了最外层的点对, 并将其用线段连接起来.

从图中我们可以看出, 我们将这个图形剖分成了一个简单多边形和一些半月. 对于这个图形, 我们只要求出简单多边形的面积再加上所有的半月的面积. 便是这三个圆形的面积并.

我们将这个做法一般话.

1.       去掉重复的圆形并求出圆与圆之间的所有交点的点集Ω.

2.       对于任意一个圆, 点集Ω中对应于这个圆的交点将其离散化成一个个小圆弧. 如果圆弧的角度大于90度, 则添加虚点, 将其分解成两个小圆弧.

3.       规定逆时针为圆弧的正方向.对于所有的小圆弧, 判断其是不是被其他圆所覆盖过. 取出所有的未被覆盖过的圆弧.

4.       对于圆弧的两个端点连接而成的线段, 将其看成简单多边形的一条边, 把其构成的有向面积加到总面积里面.

5.       对于圆弧所构成的半月, 将其面积直接加到总面积里面.

判断小圆弧是不是被其他的圆覆盖的方法, 可以取出这个圆弧的特征点(比如圆弧的中点), 然后判断这个点是不是被其他圆所覆盖.因为小圆弧是用所有交点离散化之后的,所以小圆弧上除了端点之外都有共同特征,因而上述方法是正确的.

这个做法是否适用于所有的情况呢? 且看如下图形:

对于这种内空的情况, 我们的做法也是适用的.因为对于内部的图形来说. 我们求得的多边形是顺时针的. 所以最后的总面积相当于减掉了这部分面积. 下面让我们来证明这个做法的正确性.

算法复杂度

对于每一个圆来说, 其圆上的点最多是O(n)个. 也就是说圆上那个最多有O(n)条小圆弧.每一个圆弧判断是否被覆盖的复杂度是O(n). 也就是说总的复杂度是O(n^3), n为圆的个数.

实际上,这样裸露的实现方法浪费了大量的有用信息,所以算法复杂度过高.我们可以通过改进圆弧是否被覆盖的方法来优化时间复杂度.

算法的优化

对于一个圆形来说,把他和所有其他圆形的交点求出来之后我们可以知道这个圆形上所有被覆盖掉的极角区间.我们可以用O(nlogn)的算法来求出极角区间的并.再用总的区间减掉这个并集,剩下的就是我们所要知道的所有未被覆盖过的小圆弧.

经过这样的优化,时间复杂度变为了O(n^2logn).而且这个logn的出现是因为区间并需要排序.如果用非基于比较的排序算法的话,时间复杂度可以降低为O(n^2).

算法的拓展

相信读者已经能够看得出, 此算法有一定的通用性. 如果把圆换成多边形, 最终算法的框架也是一样的. 只是细节上会有所变化.甚至可以是求圆和多边形等混合图形的并集.

 那天志旭看到上海赛区的题目挂到spoj上面了. 我也突然来了兴致, 想看看这道题目是不是和我想的一样. 说实话,这道题目其实就是我们校赛预赛的那道三维照相机的题的简化版本+最大独立集.

比赛现场我还在想我们学校的那两个队伍应该有最少有一个会搞这道题. 没有想到他们都怕40个点的最大独立集会超时...不敢去做这道题目. 真是faint. 碰上个原题, 居然不敢做.

很明显这道题目的数据很难出的很强. 才40个点, 明显就是让你暴力过去的.

嗯...不废话了. 说说题目解法.

几何部分的核心就是求出三维三角形的遮挡关系.

这一部分可以这样求: 对于每一个三角形, 从原点开始对三个点分别做三条射线. 这样就包含出了一个无限的空间. 那么怎么判断这些无限空间是不是有相交呢?

一对空间的3 * 3 == 9对"面"如果有相交的话, 那么这对空间就一定相交了. 否则只剩下包含的情况.

包含的情况只要在某个空间取出一个点, 看看是不是在另一个空间之内就好了.

 矩阵真的好优美，好多在数学中那些乘乘加加的操作，其本质都是矩阵。这些操作，往往都是把事物进行分解，对每一个基量进行操作，最后再把这些操作整合起来。

向量旋转，这个几何中的基本操作，可以相当优美的用矩阵来操作。究其原因，也是因为向量是多维的。用矩阵来操作，正是把向量分解开来，分别旋转，最后再进行整合。

看下面的矩阵

这个是二维向量的旋转矩阵，它可以将一个向量逆时针旋转一个角度。

将其变形，变会得到二维向量的顺时针旋转的形式：

这里要注意一种特殊的情况，就是当角度为90度的时候，sin和cos的结果只有1, 0, -1三种可能性。所以这个矩阵可以改写成特殊的形式，其意义在于用这样的旋转操作，不会产生精度问题。sin和cos的运算的精度是比较低的，能少用则尽量少用。在计算几何中的向量旋转操作，大部分都可以通过变形，只用到旋转90度，从而避免精度问题。

再来说一点就是，这些旋转矩阵都有一些特点，最明显的莫过于他们的行列式的值都是1。所以在验证正确性的时候，可以用这个操作。也正因为有这一个性质，所以向量才只会进行旋转，不会进行缩放。

三维向量的旋转矩阵：

上面三个公式的旋转方向可以看成按右手定则。

来看第三个公式，这个公式是围绕Z轴，把X轴往Y轴方向移动。我们把拇指向上（表示Z轴），手指指向X轴，然后手指自然弯曲方向便是旋转方向。

其它两个公式也是类似。

其实第三个公式，去掉Z轴，就是开头讲的逆时针旋转的公式。

在其它方向上的旋转都可以由这三个矩阵组合而来。

围绕轴u = (ux, uy, uz)来旋转的矩阵代码如下：

double a[3][3] = {
        {SQR(ux) + (1 - SQR(ux)) * c, ux * uy * (1 - c) - uz * s, ux * uz * (1 - c) + uy * s},
        {ux * uy * (1 - c) + uz * s, SQR(uy) + (1 - SQR(uy)) * c, uy * uz * (1 - c) - ux * s},
        {ux * uz * (1 - c) - uy * s, uy * uz * (1 - c) + ux * s, SQR(uz) + (1 - SQR(uz)) * c}
    };

要注意这个ux * ux + uy * uy + uz * uz = 1

有一个比较有意思的问题就是，知道旋转矩阵之后，怎么来确定向量u呢？

我们做如下变形之后，可以得到：

Ru = Iu –> (R – I)u = 0

也就是说我们要找到一个非0的向量，使得他和一个矩阵乘起来得到一个空矩阵。这个问题可以用高斯消元来解决。实际上我们就是要解一个线性方程组。

 题目连接：http://www.topcoder.com/stat?c=problem_statement&pm=10516&rd=13900

昨天做SRM再次失败，只做出了第一道题。每次做500分都差一点。郁闷的要死，昨天又是死活不过样例，今天醒来想一想，有一个细节方面还没有想清楚就急于去写了。导致算法上有很大的纰漏。

实际上这题算法还是挺容易想的，不过前提是要对矩阵乘法比较了解。实际上这道题也是代表了矩阵乘法的一种类型。我们比较常接触的是那种用乘法和加法的矩阵。实际如下替换之后，矩阵的各种性质也是保持的：

乘法-->加法

加法-->取最大值

这种矩阵，我们的乘法操作是如下的：

 //假设我们是要把Matix A * Matix B的结果存到Matix ans中
 for (i = 0 to n  -1 )
      for (j = 0 to n – 1)
          ans[i,j] = minValue;
          for (k = 0 to n – 1)
                 ans[i][j] = max(ans[i][j], a[i][k] + b[k][j])
从这种操作的意义上来看，就是用来取最长路之类的。跟本题是一样的。

这个题目特殊的地方在于，它有两个要求，一种是必须走K步，中间不可以停下，另一种就是中间可以停。

比赛时我没有看清楚这个条件，以为都是可以停的，所以直接按最原始的做法来做的，等我反应过来看错题的时候，又太急了，没有想清楚就乱去写了，导致算法写反了。

算法如下:

首先我们构造原始矩阵A，A就是由输入的那三个参数来的，但是要加一种情况就是如果两点不可达的时候，要把值设置成无穷小。而不是题目里的0.

然后我们求A = A^stepsPerSecond。这样便可以求出走这些步之后的情况。

再下一步我们不可以直接求A^timeLimit，为什么呢？这是因为我们中间是可以停下的。为了处理这种情况，我们可以把A[1,1]设置为0。这样我们便可以求得最终的答案了。不过这里要注意A[1,1]有可能本来是大于0的，这个时候就不用管它了。不要把这里也设成0。

这种矩阵还有一点和普通的不同在于它的单位矩阵并不是对角线全是1。而是对角线全是0，其它的全是无穷小。这样的矩阵和另一个矩阵相乘之后才可以保持另一个矩阵的不变。

上面如果没有看明白，就直接看下面的代码吧，代码还是比较清楚的：

public class AntOnGraph
{
    static int n;
    public string maximumBonus(string[] p0, string[] p1, string[] p2, int stepsPerSecond, int timeLimit)
    {
        n = p0.Length;
        long[,] st = new long[n, n];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                int k = (int)(p0[i][j] - '0') * 100 + (int)(p1[i][j] - '0') * 10 + (int)(p2[i][j] - '0');
                k -= 500;
                if (k == -500) {
                    st[i,j] = long.MinValue;
                } else {
                    st[i,j] = k;
                }
            }
        }
        st = mypow(st, stepsPerSecond);
        if (st[1,1] < 0) {
            st[1,1] = 0;
        }
        st = mypow(st, timeLimit);
        if (st[0,1] == long.MinValue) {
            return "IMPOSSIBLE";
        } else {
            return st[0, 1].ToString() ;
        }
    }
    public long[,] mypow(long[,] a, int b)
    {
        long[,]ans = new long[n, n];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == j) {
                    ans[i,j] = 0;
                } else {
                    ans[i,j] = long.MinValue;
                }
            }
        }
        for (; b != 0; b >>= 1) {
            if (b % 2 != 0) {
                ans = mul(ans, a);
            }
            a = mul(a, a);
        }
        return ans;
    }
    public long[,] mul(long[,] a, long[,] b) {
        long[,] c = new long[n, n];
        for (long i = 0; i < n; ++i) {
            for (long j = 0; j < n; ++j) {
                c[i,j] = long.MinValue;
                for (int k = 0; k < n; ++k) {
                    if (a[i,k] > long.MinValue && b[k,j] > long.MinValue) {
                        if (a[i,k] + b[k,j] > c[i,j]) {
                            c[i,j] = a[i,k] + b[k,j];
                        }
                    }
                }
            }
        }
        return c;
    }
}